While making a raytracer in Rust, I needed an efficient way to store the pixels of a 2D image. In this post, we'll compare two different implementations of a 2D grid datatype, dipping our toes into data parallelism with Rayon and benchmarking with Criterion.

Oh, and all the code I reference here is on GitHub.

Defining the Grid trait

The Grid API is pretty minimal. For my ray tracer, I just need a way to set each pixel's colour, and then a way to read each pixel's colour when it's time to generate the .PNG file.

Firstly, we need a way to index this grid. A simple Point type will do.

/// A point used to index a 2D grid.
#[derive(Clone, Copy)]
pub struct Point {
    pub x: usize,
    pub y: usize,
}

Consumers of our grid library can use Point to refer to elements in the grid, for getting and setting. Speaking of setting, in my particular use-case, the value stored at each point in the grid can be calculated completely independently of each other. Calculating each pixel in an image is an embarrassingly-parallel problem. So, let's make the setter parallel. Don't worry, I promise Rust has a library to make this trivial. "Fearless concurrency" is a selling point of Rust for a reason.

/// A container which stores elements at 2D points.
pub trait Gridlike<T> {
    fn width(&self) -> usize;
    fn height(&self) -> usize;

    /// Get the element at the given point.
    fn get(&self, p: Point) -> &T;

    /// Set all elements of the grid, using a setter function.
    /// The setter function takes a point and returns the value which should be
    /// assigned to the grid at that point.
    fn set_all_parallel<F>(&mut self, setter: F)
    where
        F: Send + Sync + Fn(Point) -> T,
        T: Send;

}

This is a very minimal API. I could add more methods, like a fn set(&mut self, p: Point, val: T) that sets the element at a particular point. But this is all I needed for my particular use-case (the raytracer). If I ever expand this into a general-purpose crate and publish it, I'll add more methods. But for now, this interface gives us enough to start implementing and benchmarking.

Implementing Grid with nested Vecs

The obvious choice for implementing this grid is to use a nested 2D Vec, i.e. a Vec of Vecs. Let's implement that in its own module under vec2d.rs. First, let's define the grid.

use crate::{Gridlike, Point};

pub struct Grid<T> {
    array: Vec<Vec<T>>,
    width: usize,
    height: usize,
}

Straightforward enough! Now, let's make a very simple initializer. In my particular use-case, I didn't really care what the initial value of each point in the grid was, because before anything had the chance to read from the grid, my ray-tracing code would write new values to it. So, let's just write the simplest constructor we can. We'll just fill the grid with whatever default value T::default() provides.

impl<T> Grid<T> {
    pub fn new(width: usize, height: usize) -> Self
    where
        T: Default + Copy,
    {
        let mut array = Vec::with_capacity(height);
        for _ in 0..height {
            array.push([T::default()].repeat(width * height));
        }
        Self {
            array,
            width,
            height,
        }
    }
}

OK, so now consumers of this library can initialize the grid. Great! Let's get to the interesting part: implementing the Grid API. The methods are very straightforward, except for set_all_parallel, which gets a little hairy:

impl<T> Gridlike<T> for Grid<T> {
    fn width(&self) -> usize {
        self.width
    }

    fn height(&self) -> usize {
        self.height
    }

    fn get(&self, p: Point) -> &T {
        &self.array[p.y][p.x]
    }

    fn set_all_parallel<F>(&mut self, setter: F)
    where
        F: Send + Sync + Fn(Point) -> T,
        T: Send,
    {
        use rayon::prelude::*;
        self.array.par_iter_mut().enumerate().for_each(|(y, row)| {
            for (x, item) in row.iter_mut().enumerate() {
                *item = setter(Point { x, y });
            }
        });
    }
}

The amazing Rayon crate is one of my favourite things about Rust. Just replace iter() with par_iter() and boom, you're parallelising iteration across all available CPU cores. I fell in love with Rust when I realized how easy it was to parallelize my code and know it will work correctly (because Rust won't compile if the iteration isn't safe to parallelize)!

This was my first attempt at writing a 2D grid. I like that it's simple and (to me) fairly intuitive to understand. The code seemed very fast when I ran it, but then again, "fast" is very subjective. In my day job, I write services that wait on HTTP roundtrips to traverse the planet. So any code that iterates over some in-memory container is going to be "fast" to me. The only fair way to judge this implementation's speed is to try writing a different implementation and compare them. How else could I implement this?

Implementing Grid with a single Vec

I remember reading some old programmer trick from the 80s, when computers were so slow that everyone had to be real fanatics about performance. The trick is basically, never use a 2D array. Instead, use a 1D array, and use some simple math to convert between 2D and 1D representations. Basically, the element stored at index i is (i%width, i/width).

Why might this be faster? Well, modern CPUs are much faster at iterating through arrays rather than following pointers, because of "data locality" (see this stack overflow for the basics). The Vec docs define Vec as "a (pointer, capacity, length) triplet. No more, no less." This means that iterating over Vec<T> will only require following a pointer once (to get to the start of the Vec). But iterating over a Vec<Vec<T>> will require n pointer follows, one for each nested vector, because they're all separate Vecs.

The 1D Vec solution is very similar to the 2D Vec solution, except we need un poquito de math to translate between the 2D representation (which callers use) and the 1D representation (which our implementation uses). You can see this in the get and set methods. Anyway, here's vec1d.rs:

pub struct Grid<T> {
    array: Vec<T>,
    width: usize,
    height: usize,
}

impl<T> Grid<T> {
    pub fn new(width: usize, height: usize) -> Self
    where
        T: Default + Copy,
    {
        Self {
            array: [T::default()].repeat(width * height),
            width,
            height,
        }
    }
}

impl<T> Gridlike<T> for Grid<T> {
    fn width(&self) -> usize {
        self.width
    }

    fn height(&self) -> usize {
        self.height
    }

    fn get(&self, p: Point) -> &T {
        &self.array[p.y * self.width + p.x]
    }

    fn set_all_parallel<F>(&mut self, setter: F)
    where
        F: Send + Sync + Fn(Point) -> T,
        T: Send,
    {
        use rayon::prelude::*;
        let width = self.width;
        self.array.par_iter_mut().enumerate().for_each(|(i, item)| {
            *item = setter(Point {
                x: i % width,
                y: i / width,
            });
        });
    }
}

Benchmarking the Grid implementations

OK, now that we have two implementations, it's time to compare them. Rust has built-in support for benchmarks, which is really lovely. If you want extra features, like nice graphs, or automatically running benchmarks multiple times and constructing a statistical model of the results, Criterion is a really easy crate for that. Also, it generates nice graphs. Fuck I love a nice graph. So do product managers. If you ever have the misfortune good luck to work with a product manager, remember: your work doesn't mean anything unless you can show them a graph of before and after the change.

We'll benchmark three different scenarios for our Grid implementations:

1. Setting all elements
2. Getting random points
3. Iterating over points

Criterion lets us run a benchmark with several different sample inputs, and across several different implementations. For example, the set_grid benchmark will use two different inputs, which correspond to mathematical difficulty. And it will use two different implementations of Grid, i.e. our vec1d::Grid and vec2d::Grid.

use criterion::{black_box, criterion_group, criterion_main, BenchmarkId, Criterion};
use rand::Rng;
const WIDTH: usize = 300;
const HEIGHT: usize = 200;

/// Some hard math operation to apply to the grid.
fn operation(difficulty: usize) -> impl Fn(Point) -> usize {
    let f = black_box(|difficulty| {
        move |Point { mut x, mut y }| {
            for _ in 0..difficulty {
                y = x + y;
                x = if difficulty >= 1 && x % 2 == 0 {
                    x.pow(2) + y
                } else {
                    x + y
                }
            }
            x + y
        }
    });
    f(difficulty)
}

/// Benchmark the `set_all_parallel` method of Gridlike.
fn set_grid_bench(c: &mut Criterion) {
    let mut group = c.benchmark_group("Set");
    let difficulties = vec![1, 5];
    for d in difficulties {
        group.bench_with_input(BenchmarkId::new("1D Vec", d), &d, |b, d| {
            let mut g = vec1d::Grid::new(WIDTH, HEIGHT);
            b.iter(|| g.set_all_parallel(operation(d.clone())));
        });
        group.bench_with_input(BenchmarkId::new("2D Vec", d), &d, |b, d| {
            let mut g = vec2d::Grid::new(WIDTH, HEIGHT);
            b.iter(|| g.set_all_parallel(operation(d.clone())));
        });
    }
    group.finish();
}
/// Benchmark the `get` method of Gridlike with random access.
fn get_grid_bench_random(c: &mut Criterion) {
    let mut group = c.benchmark_group("GetRandom");
    let point = || Point {
        x: rand::thread_rng().gen_range(0..WIDTH),
        y: rand::thread_rng().gen_range(0..HEIGHT),
    };
    for d in &[1, 10, 100, 1000] {
        group.bench_with_input(BenchmarkId::new("1D Vec", d), &d, |b, d| {
            let mut g = vec1d::Grid::new(WIDTH, HEIGHT);
            g.set_all_parallel(operation(1));
            b.iter(|| {
                for _ in 0..**d {
                    black_box(g.get(point()));
                }
            });
        });
        group.bench_with_input(BenchmarkId::new("2D Vec", d), &d, |b, d| {
            let mut g = vec2d::Grid::new(WIDTH, HEIGHT);
            g.set_all_parallel(operation(1));
            b.iter(|| {
                for _ in 0..**d {
                    black_box(g.get(point()));
                }
            });
        });
    }
    group.finish();
}
/// Benchmark the `get` method of Gridlike, accessing elements in a predictable order.
fn get_grid_bench_order(c: &mut Criterion) {
    let mut group = c.benchmark_group("GetOrder");
    for d in &[1, 50, 100, 200] {
        group.bench_with_input(BenchmarkId::new("1D Vec", d), &d, |b, d| {
            let mut g = vec1d::Grid::new(WIDTH, HEIGHT);
            g.set_all_parallel(operation(1));
            b.iter(|| {
                for x in 0..**d {
                    for y in 0..**d {
                        black_box(g.get(Point { x, y }));
                    }
                }
            });
        });
        group.bench_with_input(BenchmarkId::new("2D Vec", d), &d, |b, d| {
            let mut g = vec2d::Grid::new(WIDTH, HEIGHT);
            g.set_all_parallel(operation(1));
            b.iter(|| {
                for x in 0..**d {
                    for y in 0..**d {
                        black_box(g.get(Point { x, y }));
                    }
                }
            });
        });
    }
    group.finish();
}

criterion_group!(
    benches,
    set_grid_bench,
    get_grid_bench_order,
    get_grid_bench_random
);
criterion_main!(benches);

You can run these benchmarks with cargo bench. Note the use of black_box to stop the compiler from optimizing away all our code. Sometimes the compiler decides that, because ultimately computing all this data doesn't have any side-effect (like printing a number to the screen, or sending it in a HTTP request), it doesn't even need to do the work at all. That's awesome for making your production binaries faster, but it's really annoying when you're trying to benchmark code.

Technically Criterion has its own subcommand, cargo criterion, which is supposed to be better, but when I try to run that I always run into this panic and I don't know how to fix it yet. But normal cargo bench works fine so I'm not very invested in debugging at this point.

Well, I ran the benchmarks on my Macbook Pro, which has an Intel Core i7-9750H CPU, and here's the results.

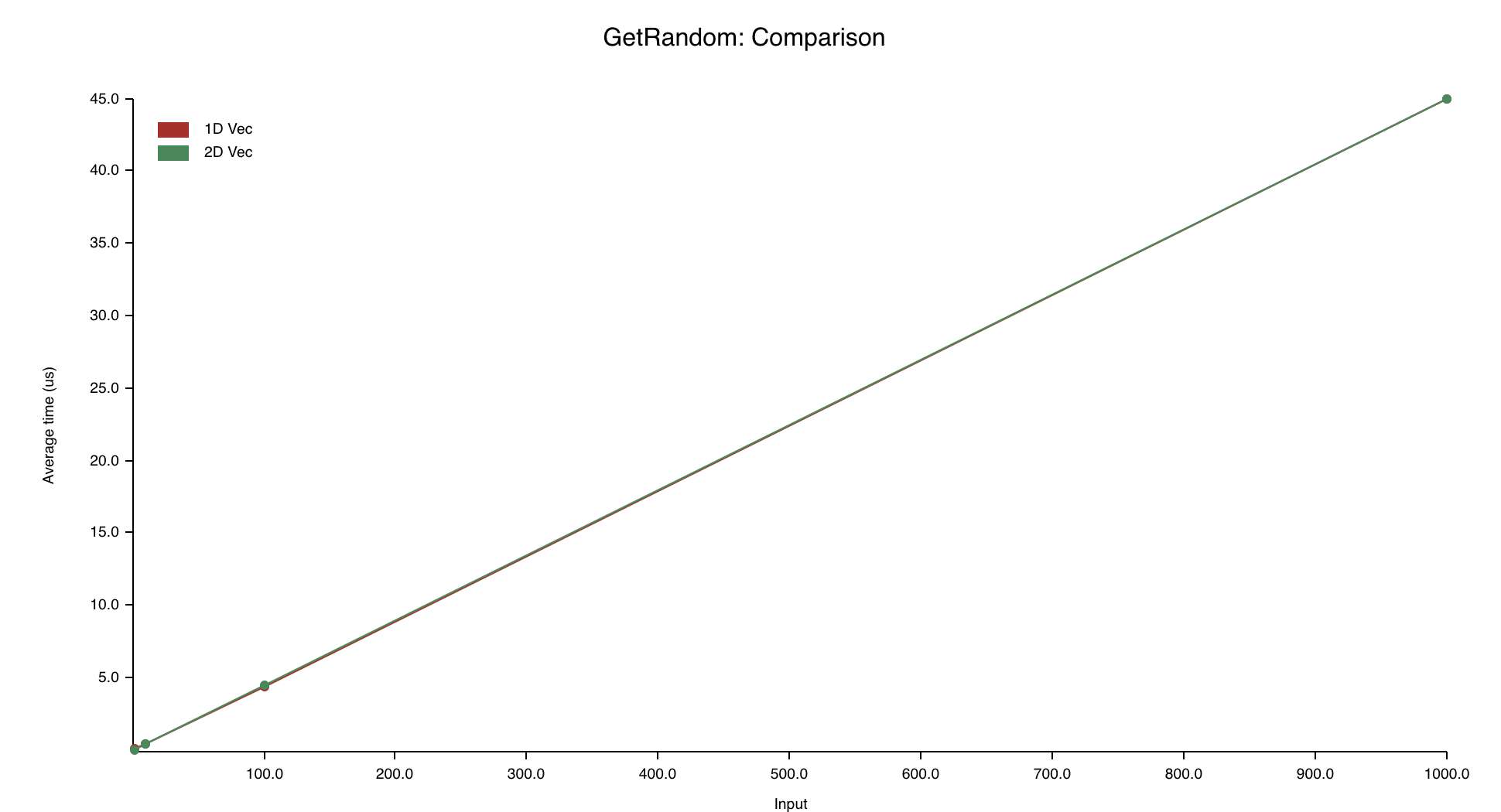
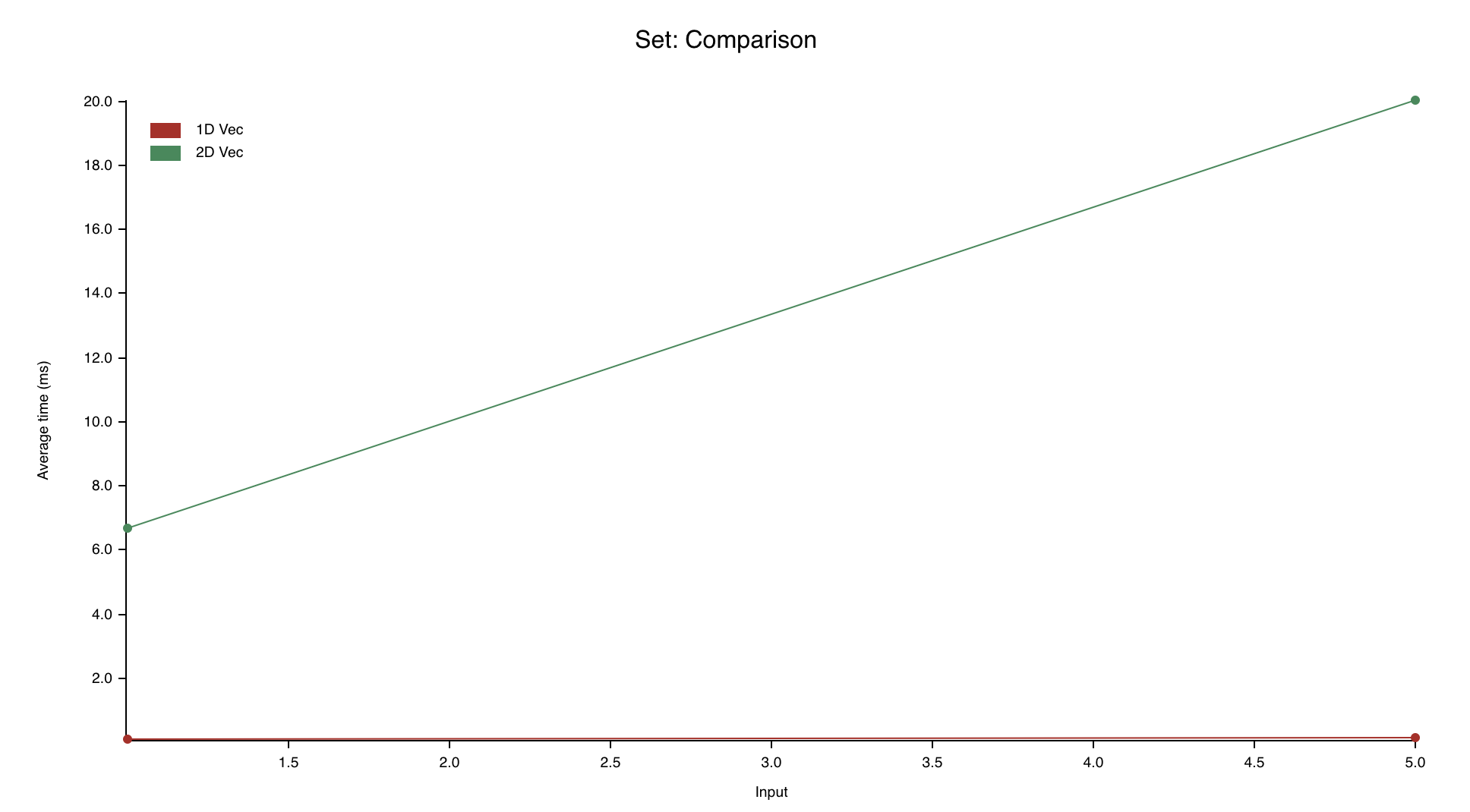
Wow. Seems like those 80s programmers really did know something. Storing the elements in 1D is way faster than storing them in 2D, even though the two implementations have the same Big O complexity. I'm glad we benchmarked it.

Note: Different CPU architectures optimize things differently! You can always clone this repo and run the benchmarks on your own machine. If this was a work project, I would make sure to benchmark this on the same machine that will run the code in production. The results might be very different!

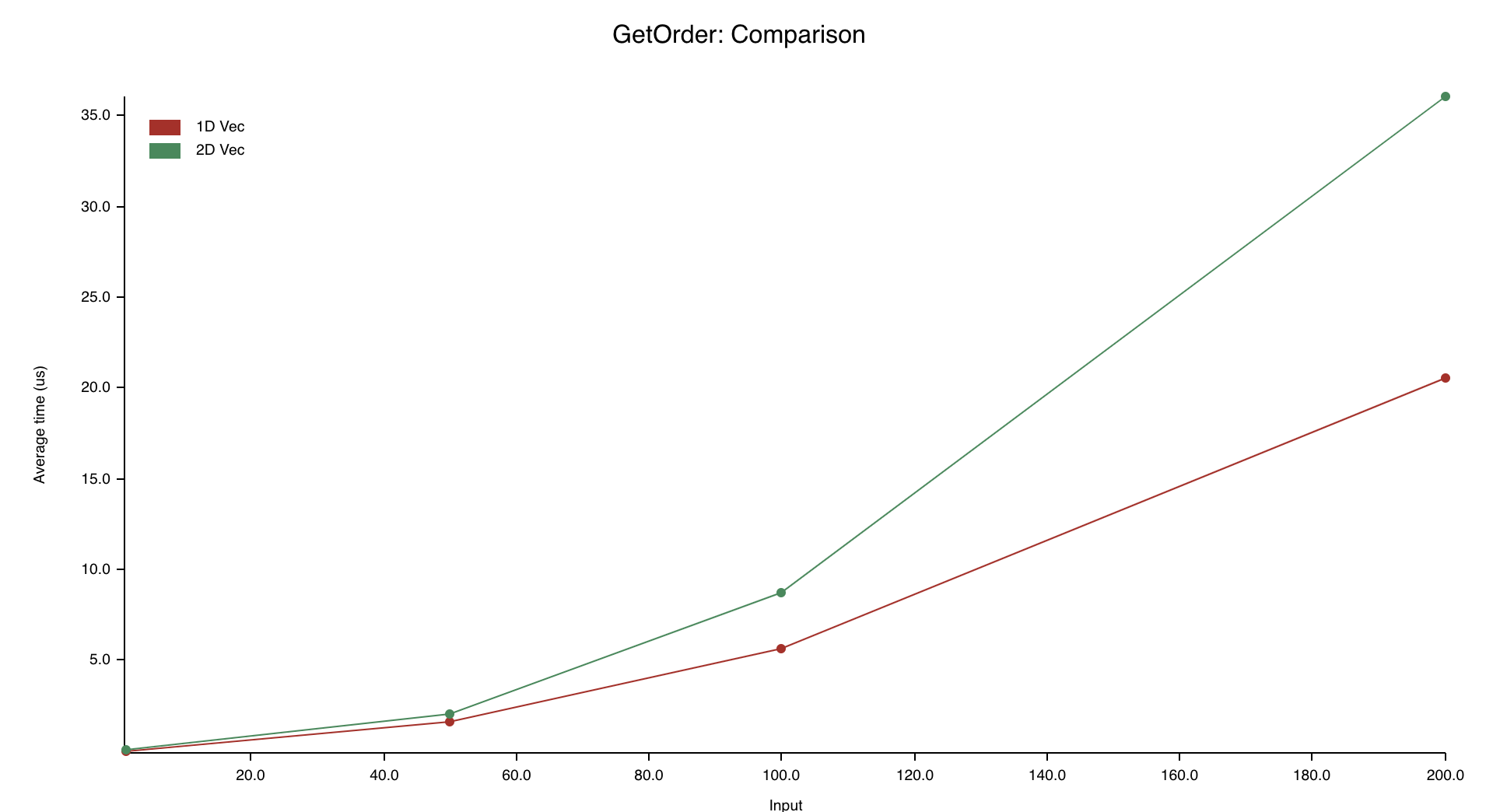
Oh, and here's a bonus graph comparing the "GetOrder" benchmark, run for both 1D and 2D Vec implementations, getting the first 1, 50, 100 or 200 elements from the grid. I'm only including it here to show you how cool Criterion is. Seriously, this crate can fit so many graph visualisations in it.

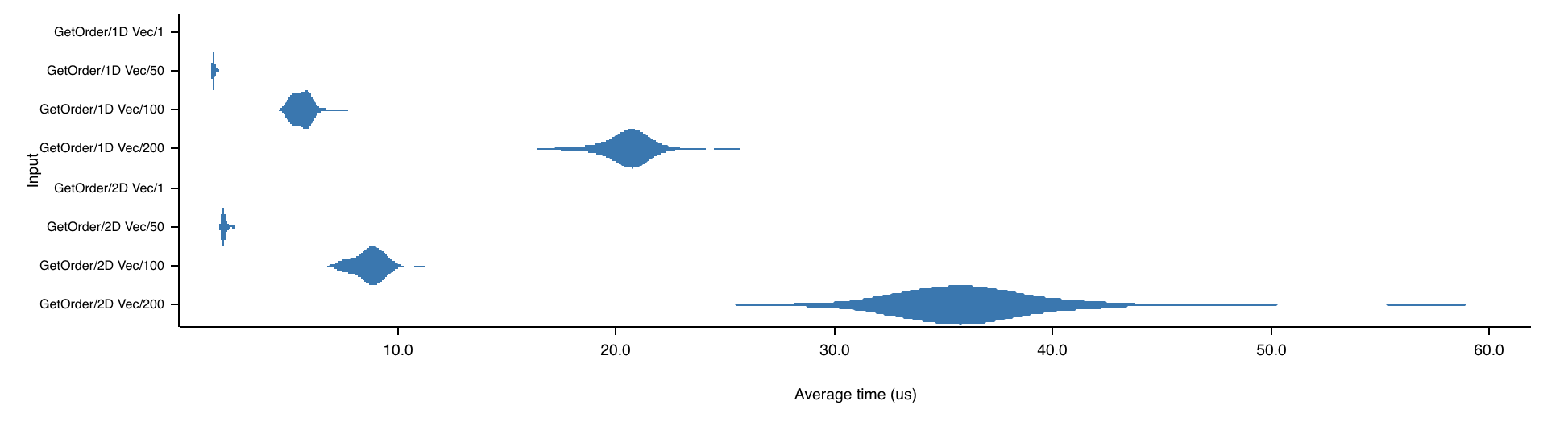
OK, so we've established that for all workloads, 1D Vec is faster than 2D Vec. But... can we do even better? Why are we even storing these elements in a Vec, which allocates memory on the heap? What if we could store them all in the stack, and avoid that allocation? In part two of this series, we'll use const generics to create a generic-sized array for representing the grid.

Thanks for reading! If you have any questions or suggestions, please let me know on twitter or via email. The code is on GitHub and if you have suggestions for improving it, feel free to open a PR. Thanks!

Thanks to Steve Klabnik and Nick Vollmar for feedback